Carta Natal online
Herramientas y recursos para el cálculo de la carta natalCómo se superan las cuadraturas
POR Jorge BosiaIntrodución
Las cuadraturas solían ser vistas como aspectos “maléficos” por los astrólogos antiguos –me refiero a los que trabajaban hace 30 años o antes-. En las últimas décadas, sin embargo, se ha comprendido cada vez más el absurdo de presentar no sólo determinados ángulos, sino cualquier otro elemento del lenguaje astrológico como “maléfico” o “benéfico”. Hoy sin duda debería resultar obvio que esos son juicios de valor que no van más allá de la nariz de quien los emite y que no tienen nada que ver con el conocimiento.
Algunos han propuesto otras terminologías para suplantar el famoso “maléfico”, por ejemplo, se dice que las cuadraturas son aspectos “desafiantes” (en una terminología que, sin duda, tienta al componente escorpiano que todos tenemos). Otros han propuesto el término “disonante”, apelando al oído musical y a la cuerda pisciana que todos tañemos de tanto en tanto. Estos términos son útiles para acercarnos a la naturaleza de este ángulo, y pueden ser usadas con menor carga de malentendidos que la de “maléfico”.
El punto de fondo es comprender qué es una cuadratura y cómo funciona. Los juicios de valor están fuera de lugar.
Si logramos comprender su significado quizá incluso podamos aspirar a “superarlas”.
“Superar” las cuadraturas
Ante todo aclaremos que “superar” no significa eliminar, aniquilar o hacer desaparecer. Usamos “superar” en el sentido en que empleó esta palabra el filósofo alemán Hegel: superar, en ese sentido es ir más allá de algo, pero conservándolo.
Superar una cuadratura implica poder ver el conflicto que ésta supone desde un punto de vista que no es ninguno de los dos extremos que lo protagonizan. Es decir, implica generar un nuevo nivel de ser desde el cual el conflicto pueda ser contenido.
Así pues, sostenemos que las cuadraturas no desaparecen, pero pueden ser superadas. A partir de su negación preservadora se puede construir otra cosa con ellas.
¿Qué es una cuadratura y cuál es su importancia?
Para poder superarlas es preciso indagar primero cuál es el sentido de las cuadraturas, lo cual implica a su vez, saber qué son y cómo funcionan.
Se habla de “cuadratura” cuando dos planetas forman un ángulo de 90º con referencia al Sol (como vértice del ángulo).
La primera cuestión que nos viene a la mente es: ¿por qué el ángulo de 90º es importante y los de 98º ó 123º, por citar cualquiera, no lo son?
La razón es que el cuadrado es una figura que tiene cuatro ángulos interiores de 90º (= 360º). El cuadrado y el círculo coinciden en esto, y debido a eso siempre se intentó lograr la “cuadratura del círculo”.
Pero ¿qué tiene de importante esto para la Astrología? Reparemos en que el cuadrado es un polígono regular, es decir, que tiene sus lados de igual longitud y sus ángulos de igual amplitud. Esto es importante porque los polígonos posibles son infinitos; pero sólo muy pocos son regulares. Y la regularidad permite extraer criterios válidos para la acción y la comprensión. Los aspectos son algunos de estos criterios.
Entre los polígonos regulares tienen mayor significación aquellos que tienen la menor cantidad de lados. Un hecho de máxima importancia es que se puede establecer una correlación simbólica entre el número de sus lados (y ángulos) y los números. Y, como todos los números se construyen sobre la base de los pri-meros nueve, son especialmente significativos los polígonos que tienen un núme-ro de lados entre 3 y 9, a los que podemos agregar el 12, pues el Zodíaco tiene una estructura dodecagonal. Y casi todos estos corresponden a los aspectos que la tradición astrológica viene utilizando más asiduamente:
De modo tal que el estudio de los aspectos nos sugiere pensar a la Astrología a partir de lo que podríamos llamar un “pensamiento geométrico”.
Los aspectos más efectivos y tradicionalmente utilizados se basan en las siguientes correlaciones entre figuras geométricas, números y aspectos:
Triángulo -> nº 3 -> Trígono
Cuadrado -> nº 4 -> Cuadratura
Pentágono -> nº 5 -> Quintil
Hexágono -> nº 6 -> Sextil
Heptágono -> nº 7 -> Septil
Octágono -> nº 8 -> Semicuadratura y Sesquicuadratura
Nonágono -> nº 9 -> Novil
Dodecágono -> nª 12 -> Semisextil y Quincuncio
¿Porqué quedan afuera el 1 y el 2? Simplemente porque no forman una figura cerrada (polígono). Sin embargo, el 1 y el 2 corresponden a los aspectos de Conjunción y Oposición respectivamente y se podrían asimilar a casos límite de los ángulos.
El hecho más significativo es que los polígonos regulares a diferencia de los que no lo son, tienen un centro equilibrado (son simétricos) y, por tanto, no sólo se pueden inscribir en el círculo, sino que se inscriben de tal modo que sus centros coinciden con los del círculo. Esto quiere decir que los vértices de los polígonos regulares son, necesariamente, puntos de una circunferencia.
La circunferencia es el caso límite de los polígonos regulares. Se la podría considerar un polígono regular de infinitos lados. A la inversa, se podría decir que los polígonos regulares son, en cuanto a sus vértices, circunferencias incompletas.
La circunferencia (que es una línea) determina un círculo (que es una figura plana). Y el círculo tiene un valor simbólico fundamental. Es el símbolo de la totalidad y, consecuentemente, de la reconciliación de todos los opuestos. En casi todas las corrientes religiosas o espirituales, el círculo ha representado ese estado supremo del ser **.
De modo que los vértices los polígonos regulares evocan inmediatamente a la circunferencia misma y, en consecuencia al círculo. Esto significa que: los polígonos regulares son recordatorios de la totalidad, aunque son, de hecho, incompletos. Esto los pone como casos paradigmáticos de lo que son los símbolos en general. Pues el símbolo es eso: algo que evoca lo perfecto; pero que, al estar en-carnado o manifiesto, es necesariamente imperfecto.
Ahora bien, como hemos indicado, los poligonos regulares tienen no sólo lados iguales sino también ángulos iguales. Esto quiere decir que un sólo ángulo de un polígono regular basta para definir el polígono completo. Por ejemplo: si tengo un ángulo de 90º, ya sé que se trata de un cuadrado; si tengo un ángulo de 72º, ya sé que se trata de un pentágono, etc.
Ciertos y determinados ángulos son, pues, representantes de los polígonos regulares. Y como los Aspectos astrológicos son ángulos, resulta evidente por qué son significativos esos ángulos y no otros.
Podría objetarse, sin embargo, que puede haber un ángulo de 90º, que fuera parte de un polígono irregular y, no obstante, inscripto en el círculo, como el polígono de la figura 1.
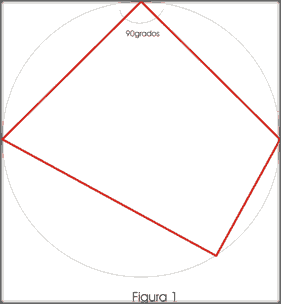
Pero de esto se trata: justamente lo interesante del ángulo de 90ª (Cuadratura) es que nos “llama” a considerar el cuadrado, y no la otra figura, que resultaría arbitraria y azarosa.
Lo que ha hecho la Astrología al destacar esos pocos ángulos es reconocer que esos ángulos nos “piden” que los completemos no de cualquier manera, sino como polígonos regulares.Algo requiere que lo hagamos así.
De hecho, quedamos mucho más “satisfechos” si completamos un ángulo de 90º con otros tres.
Y esto es así porque en el cuadrado dibujado o imaginado “resuena” la totalidad inalcanzable.
Y esta resonancia se traslada también al ángulo de 90º que lo representa.
Como principio de la percepción y del conocimiento en general, el principio implicado aquí (la tendencia a completar la forma), ha sido detenidamente estudiado por los psicólogos guestálticos de principios del Siglo XX. Ellos le dieron un alcance gnoseológico y psicológico; nosotros preferimos entender este principio como uno de los indicios que apuntan a la suposición de lo inefable (Dios); pero no entraremos aquí a desarrollar este punto.
¿Cómo funcionan las cuadraturas?
Lo que hace decir a los astrólogos antiguos que la cuadratura es “maléfica” es que ésta constituye un obstáculo para que las funciones representadas por los Planetas *** puedan armonizarse entre sí, con lo cual tampoco pueden fluir adecuadamente cada uno de los planetas en sí mismo.
Esto es cierto, ¡lo que ocurre es que no es “malo”!... ¡Ni “bueno”!
Las cuadraturas pueden entenderse como un símbolo de cierto funcionamiento inarmónico de la personalidad o de ciertas tendencias pobres y conflictivas en la conducta.
Tomemos una cuadratura entre Saturno y Urano. Puede entenderse como una dificultad relativa a las funciones representadas por ambos Planetas. Así, si vemos a Saturno como la capacidad para obrar con eficacia y a Urano como la capacidad de innovar, esta cuadratura será un indicio de que la persona tiene dificultades para poner en juego satisfactoriamente ambas cosas a la vez. Va a sentir, no sin frustración, que si se mueve dentro de sus márgenes aceptados de eficacia, no puede innovar. O que si se lanza a innovar, tiene que lidiar con una angustiosa sensación de ineficacia. Como resultado, probablemente, obrará menos innovadoramente de lo que es capaz, y con mayor ineficacia de lo que desearía, y entonces, su conducta será rígida, extemporánea, etc.
Para comprender el funcionamiento de las cuadraturas, entonces hay que asumir:
1. que los planetas simbolizan funciones de la personalidad; y
2. que pueden operar satisfactoriamente o no.
Este último caso es típico de las cuadraturas. Tanto es así que se puede decir que si hay cuadratura, entonces los Planetas funcionarán insatisfactoria-mente.
Lo insatisfactorio sobre el funcionamiento de los Planetas en cuadratura se debe a que no pueden integrarse adecuadamente a la conducta. Las cuadraturas implican una dificultad de integración extra, un plus de dificultad.
En nuestro ejemplo, en tanto Urano funcione disociado de la conciencia, la capacidad de innovar se le aparecerá al sujeto como sorpresa inesperada que desbaratará sus planes, por ejemplo. Y Saturno, también disociado, lo hará como un límite externo que le impide concretar sus propósitos.
Agregaremos entonces que para comprender las cuadraturas hay que considerar que:
3. los planetas en cuadratura tienden a no integrarse a la conciencia (y por tanto a funcionar inadecuadamente en la conducta).
Pero hay algo más: el punto clave consiste en que la cuadratura puede entenderse más a fondo si asumimos que el Planeta más lento es el más difícil de integrar por naturaleza. De modo que podemos usar al planeta más lento como punto de partida tanto de nuestra comprensión del mecanismo de la cuadratura como de su superación.
En efecto, se puede decir que:
1. el Planeta más lento de la cuadratura funcionará disociado de la conciencia. Y
2. la disociación del más lento, obstruye a su vez toda posibilidad de integración adecuada del otro a la conducta.
En nuestro caso, Urano disociado no permitirá tampoco a Saturno funcionar integradamente.
Por tanto, la llave para la superación de las cuadraturas se encuentra en el Planeta más lento: las cuadraturas se superan encarando la integración conciente a la conducta del Planeta más lento.
Situemos ahora el ejemplo en una Carta natal real. Pertenece a una persona cuyo planteo de la situación, en síntesis, fue el siguiente:
“...voy a viajar a Inglaterra con mi esposa la semana que viene; vengo planeando este viaje desde hace meses; pero ayer me entero de que la autorización que tiene que darme el juez para salir del país puede tardar más de una semana. Mi mujer se enojó y me acusa de que, sabiéndolo desde hace mucho tiempo, haya dejado este trámite para último momento”.
Este es un caso real que analizamos en una clase. Pronto nos dimos cuenta que, más allá de otros factores que estaban en juego, podía ser muy interesante para esta persona aprovechar esta situación para aprender acerca de su cuadratura Urano-Saturno.
Con lo que hemos avanzado hasta aquí ya hubiese sido instructivo tanto para el sujeto como para todos. En efecto, la persona hubiera comprendido que el punto crítico está en una falta de integración conciente de Urano a su conducta. Esto es lo que se le aparece como imprevistos o sorpresas de último momento que le ponen limitaciones a sus propósitos.
Esto había aparecido, por lo demás, en muchas ocasiones a lo largo de la vida de esta persona.
Por tanto, hallando nuevas formas de integrar la creatividad y la innovación, tendría oportunidad de integrar también de una forma más acabada a Saturno, obrando con más seguridad y eficacia en la concreción de sus planes.
El hecho de comprender esto ya es un inestimable avance para la superación de la cuadratura. Claro está que deberá resolverse en la vida real; pero la claridad de conciencia respecto de su funcionamiento equivale a superar la mitad del problema.
Es decir, si la persona de nuestro ejemplo comprende que es la función de Urano la que instala el problema, se dará cuenta que debe prestar atención a Urano si quiere superar las consecuencias desagradables y esterilizantes de la cuadratura. Esto ya es un gran avance: sabemos a dónde mirar y por dónde empezar.
Pero las cuadraturas dicen todavía mucho más que eso.
Las cuadraturas como “programas” a realizar
Lo que sostendremos ahora es que la cuadratura no sólo describe los hechos, sino que indica un verdadero programa de vida.
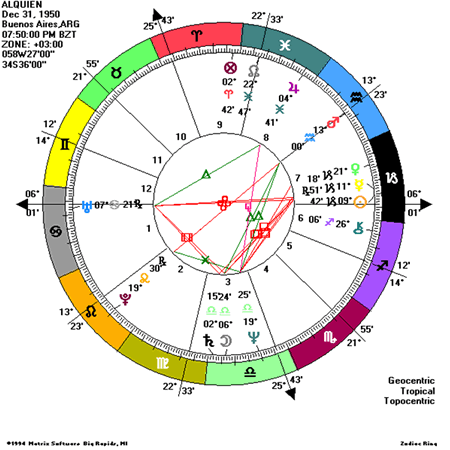
Consideremos la cuadratura que venimos usando como ejemplo, situándola ahora en la Carta Natal de la persona (Ver la Carta al final de este artículo). Se trata de la cuadratura entre Urano en Cáncer en la Casa 1 y Saturno en Líbra en la Casa 3.
Según lo que venimos desarrollando, el funcionamiento disociado (al menos en algunos aspectos) de Urano, es lo que obstaculiza integrar también a Saturno.
En efecto, la persona manifestó:
“a menudo he tenido situaciones en la vida cuando emprendo algo nuevo, en las que me veo sorprendido por imprevistos de último momento que me complican o, en algunos casos, me desbaratan completamente los planes”
Es decir: esta persona varias veces ha tenido dificultades para concretar sus planes que lo toman por sorpresa; en especial si se trataba de cuestiones que involucraban asociaciones, matrimonio o cuestiones judiciales, y en relación con actividades comerciales –sus dificultades para abandonar el país provienen de un antiguo problema comercial-. Por supuesto, se admiten otras variantes interpretativas, éstas son sólo a título de ejemplo; pero tienen el valor de que fueron con-firmadas por el sujeto.
La clave aquí es el funcionamiento de Urano. La ruptura de sus planes, el quiebre de sus objetivos, es una manifestación disociada de Urano que obstaculiza a Saturno, el que, en consecuencia, tampoco puede integrarse.
Indagando en el problema concreto que se planteaba, quedó rápidamente en claro que esta persona al planificar sus acciones no consideraba la posibilidad de imponderables, de imprevistos. Rechazaba los imprevistos, haciendo sus planes como si nunca nada de este tipo pudiera ocurrirle.
Por cierto, había otra cuestión significativa. Esta persona sabía que ese trámite estaba pendiente ¡desde hacia años! Pero no lo tomó en cuenta hasta que fue a renovar su pasaporte, pocos días antes de viajar. Se diría que “buscó” semi-concientemente lo imprevisto. Este fenómeno es algo generalizado: quien observa el comportamiento de la cuadratura de otra persona lo ve dirigirse casi de cabeza contra el obstáculo.
Todo ocurre como si hubiera una tendencia a la búsqueda de la integración. Es cierto que la disociación es inevitable; pero también lo es la contratendencia a integrarse.
Por eso las cuadraturas no sólo describen ciertos funcionamientos disociados, sino que son “programas” de aprendizaje; que nos impulsan a integrarnos. Por eso esta persona “buscaba” caer en estas situaciones: buscaba integrar a ciegas a Urano y, por tanto, también cambiar la forma de funcionar de su Saturno.
Pero ¿por qué la cuadratura hace que funcione disociado Urano?
Indagando en su vida, podía llegarse a una situación muy traumática vivida en su primera infancia relacionada con lo imprevisto. Experiencia que cargó a todo lo imprevisto de dolor; lo cual sin embargo –y esto debe enfatizarse- no es la causa de las situaciones posteriores, sino la primera manifestación de la cuadratura.
Funcionar disociado es otro modo de decir proyectado. La persona no quería saber nada con lo imponderable, lo había sacado del cuadro de la conciencia. Y disociaba ante todo a Urano porque el planeta más lento es siempre el más dificil de integrar, el que requiere más esfuerzo. Esta es la razón. Aunque de un modo también muy pobre, el grado de integración de Saturno era mayor que el de Urano porque Saturno es más fácil que aquél de ser integrado a la personalidad.
Las cuadraturas son, en consecuencia, un indicio infalible de dos fuertes proyecciones psicológicas: ante todo la de la función simbolizada por el Planeta más lento; y luego también de la simbolizada por el otro.
Esta es una regla general: cuanto más lento (o más lejano) es un Planeta, más ajeno nos resulta aquello que simboliza y más proyectado se encontrará. Este principio de interpretación es esencial en el caso de las cuadraturas. Si tratamos de superar la cuadratura a partir del Planeta más rápido no lo lograremos. Es necesario buscar en qué sentido está disociado o proyectado el más lento y, luego a partir de la integración de éste, captar lo que ocurre con el más rápido.
En nuestro caso, por ejemplo, si nuestro sujeto intentase hacer más riguroso su plan, se volvería más rígido, y el problema se agravaría. Mientras no se diera cuenta que el punto flojo consiste en incluir lo imprevisible en el plan, es decir, dejar lugar para lo imprevisible, no podrá superar esta manifestación de la cuadratura. Pero él teme lo imprevisible; entonces lo niega. No obstante, al mismo tiempo lo busca; pues la tendencia a la integración es tan fuerte como la otra y las situaciones se suceden hasta que aprende.
¿Qué ocurre con las cuadraturas una vez que se superan?
¿Qué pasa con la cuadratura si la persona integra la cualidad o la función disociada correspondiente al Planeta más lento? La pregunta es pertinente porque la cuadratura no desaparece del mapa natal: los planetas siguen estando en ángulo de 90º. Pero ocurre que si hace conciente esta disociación e integra concientemente al planeta más lento, la persona contendrá como algo interno la contradicción. O, para decirlo más fácilmente: se hará cargo de ella concientemente. Lo que era un contratiempo, un obstáculo sorpresivo que impedía concretar planes y objetivos se transforma en sabiduría acerca de la organización y la acción.
En otras palabras, la cuadratura deja de ser un problema personal de ese individuo, para pasar él a ser alguien capaz de vérselas con ese tipo de cuestión a nivel colectivo. La cuadratura se convierte así en símbolo de una responsabilidad: cuando se trate de organizar va a ser convocado y tendrá que hacerse cargo. Ese es el “resto” de cuadratura que queda. Pero deslindada ya de la problemática individual y transformada en dificultad colectiva o universal de la que el sujeto en cuestión tiene que responsabilizarse frente a sus semejantes.
Las cuadraturas son, pues, llamados a aprender a resolver problemáticas universales de la humanidad. Duelen en lo personal a fin de que el individuo no se distraiga del asunto y se ocupe. Para hacerse cargo a nivel colectivo, debe resolver el desafío en el nivel personal, así se “descarga” el problema en ese nivel y el individuo puede decir que ha “superado” la cuadratura en ese nivel, colocándola en el plano inmediato superior.
En realidad nunca nos liberamos absolutamente de la cuadratura, sino que hacemos el trabajo de llevarla desde el plano individual hasta el colectivo. Pero ese salto es muy importante y la “resuelve” para la vida individual.
¿Cómo entran en la superación de las cuadraturas nuestras ideas acerca de los polígonos regulares? Veamos.
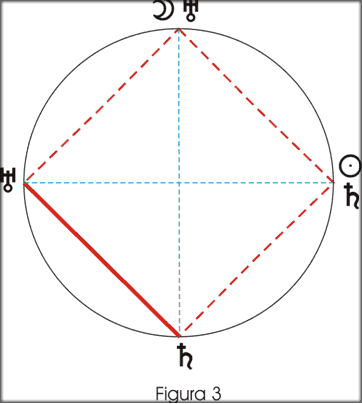
Un cuadrado tiene dos diagonales, de modo que si las trazamos en nuestra cuadratura obtendremos dos puntos opuestos, uno a Urano y otro a Saturno. La hipótesis que proponemos sugiere que, tomándonos en serio que la cuadratura remite al cuadrado, supongamos que en los vértices opuestos a los dos Planetas, opera las cualidades complementarias de éstos. Así, opuesta a Saturno se hallará una “Luna virtual” o un “Urano virtual” (opuestos “naturales” de Saturno), y opuesto a Urano se encontrará un “Saturno virtual” y un “Sol virtual” (opuestos “naturales” de Urano).
Dibujemos en lo que se refiere a este aspecto los Planetas imaginarios o vir-tuales que completan el cuadrado (Figura 3). Lo que afirmamos es que situarse (con la conciencia y la conducta concreta) en la posición de esos planetas imaginarios nos permite estar en las mejores condiciones para superar la cuadratura. Esas posiciones imaginarias o virtuales ayudan a comprender lo que está en juego y favorecen la resolución.
En nuestro caso, proyectar el componente inprevisible de las acciones personales (Urano en Casa 1) implica descargar la propia responsabilidad (Saturno virtual) en otros: cónyuge, juez (Casa 7), quienes deberán cargar (Capricornio) con el peso de la imprevisión del sujeto, y al que seguramente le recriminarán duramente esta actitud o le impedirán viajar (nuevamente Saturno virtual).
Por el lado de la otra oposición virtual, quedará totalmente opacada la posibilidad de cuidar (Luna virtual) el viaje (Casa 9); o engendrar (Luna virtual) una visión de largo alcance (Casa 9).
Es decir: las oposiciones virtuales indicarán consecuencias indirectas de la cuadratura. Pero, si se toma conciencia de tales oposiciones y su significado, se cuenta con herramientas inmejorables para superarla.
Así, nuestro sujeto, debería considerar que las observaciones y límites que vienen de parte de su cónyuge o del juez no son otra cosa que el reflejo de su propia autoconciencia (Sol) y de su propia eficacia (Saturno) y, por ende, algo a tomar muy en cuenta.
Por otro lado, ponerse en una perspectiva (Casa ) más cuidadosa (Luna), pero a la vez, tomar en cuenta lo imprevisto (Urano), equilibraría los peores frutos de su cuadratura.
Resumiendo, el papel del cuadrado, en tanto polígono regular correspondiente a la cuadratura, es el de proponer contrapolos virtuales tales que, tomándolos en consideración, ayudan a que se superen las formas primarias o pobres del aspecto.
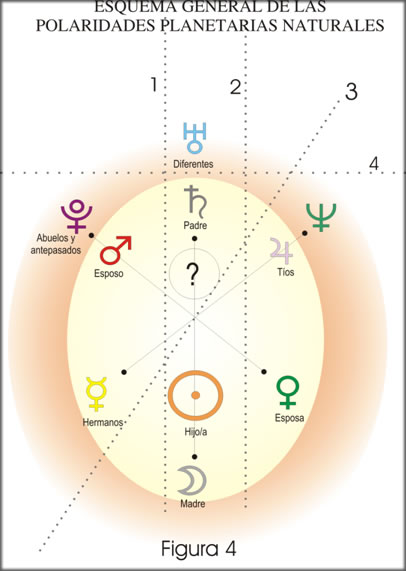
Para poder generar los contrapolos virtuales se habrán de tomar en cuenta las “polaridades naturales”. Llamamos así a aquellas que surgen del contenido simbólico de los Planetas, con independencia de su posición relativa en una Carta natal.
Proponemos como “polaridades naturales” las que expone la Figura 4.
Por ejemplo, si se trata de una cuadratura entre Neptuno y Venus, los Planetas polares a considerar serían: para Neptuno Mercurio, Marte y Saturno; y para Venus Marte y Plutón.
El intérprete deberá considerar todas las polaridades en juego y, eventualmente apoyarse en la que considere más pertinente. Esto le dará una inmejorable herramienta para ayudar a superar la cuadratura.
* Artículo publicado originalmente en la revista Médium-Coeli.
** Aún considerando que en el cielo no es el círculo la figura predominante, sino la elipse; hecho de suprema importancia, el círculo puede tomarse como una imagen de la totalidad; sobre todo teniendo en cuenta que el círculo es sólo un caso particular, y raro, de elipse.
*** Por supuesto que pueden considerarse cuadraturas a otros puntos sensibles del mapa celeste; pero me refiero a los Planetas para abreviar.
Autor: Jorge Bosia
jorge@trenkehue.com
Web: https://www.trenkehue.com
Este artículo pertenece a su autor y puede tener algunos derechos reservados.
Consulte con el autor para su publicación



