Carta Natal online
Herramientas y recursos para el cálculo de la carta natalAspectos en Astrología. La difícil convivencia de dos modelos teóricos distintos, pero no tanto
POR Julián García VaraHay dos modelos distintos de relaciones entre planetas conviviendo en la teoría moderna de los aspectos, y debemos separarlos convenientemente para evitar enredarnos en complicaciones innecesarias. Podríamos decir, sin afinar demasiado, que en astrología se entiende por "aspecto" el modo en que los efectos de dos planetas se combinan o modifican mutuamente en función de los lugares que cada uno de ellos ocupa en el zodiaco en un momento dado. Si definimos la posición de cada planeta únicamente por el signo del zodiaco que ocupa estaremos usando el modelo de aspectos por signo. Si definimos la posición relativa de un planeta respecto de la posición de otro por el número de grados que los separa estaremos usando el modelo de aspectos por arco.
El modelo de aspectos por signo
El modelo de aspectos por signo está prácticamente fuera de uso en la actualidad, salvo en la astrología india, que todavía lo conserva. François Labat (L'Astrologie nouvelle: essai de reconstitution de la véritable astrologie des Anciens, 1961) ha defendido que este fue el sistema de aspectos original, el más antiguo y consistente, y, en consecuencia, propone el abandono del sistema de aspectos por arco y su sustitución por el modelo de aspectos por signo. Este modelo es categorial, en el sentido de que los diferentes aspectos se constituyen a partir de las principales categorías usadas para clasificar los signos según su tipo. Estas categorías son la polaridad, el elemento y la modalidad. Según la polaridad, los signos se dividen en masculinos o diurnos y femeninos o nocturnos. Según el elemento, los signos pueden ser de fuego, de tierra, de aire o de agua. Y según la modalidad, los signos pueden ser cardinales, fijos o mutables.

De acuerdo con esto, dos planetas están en:
- CONJUNCIÓN, si están en el mismo signo o, lo que es lo mismo, si comparten polaridad, elemento y modalidad.
- OPOSICIÓN, si ocupan signos que comparten polaridad y modalidad, pero no elemento.
- TRÍGONO, si ocupan signos que comparten polaridad y elemento, pero no modalidad.
- CUADRATURA, si ocupan signos que sólo comparten la modalidad.
- SEXTIL, si ocupan signos que sólo comparten la polaridad
Si dos planetas están en signos que no comparten nada se dice que no se miran o que están inconjuntos, lo que equivale a decir que no hay aspecto entre ellos.
En este sistema no se tiene en cuenta la distancia en grados entre los planetas, sino solamente las categorías de las que participan según los signos que ocupan. Si se aceptan las categorías mencionadas y se entiende que cada planeta mezcla su naturaleza con la del signo que ocupa, se sigue naturalmente que dos planetas cualesquiera tendrán más o menos facilidad para sintonizar entre ellos dependiendo de los signos que ocupen. Si estos signos tienen buenas relaciones entre sí los planetas que los ocupan también las tendrán, o, al menos, verán mejoradas las posibilidades de tenerlas, y al contrario si las relaciones entre los signos son malas.
Este es un modelo esencialmente cualitativo montado sobre una estructura sectorial o territorial con límites perfectamente definidos. El planeta está en un signo o está en otro y, por tanto, formará un aspecto u otro o ninguno con cada uno de los demás planetas, pero nunca hará dos aspectos a la vez con el mismo planeta. Las relaciones son del tipo todo-o-nada, se dan o no se dan, sin matices ni graduaciones. El contexto (el signo) tiene prioridad sobre el planeta.
El modelo de aspectos por arco
El modelo de aspectos por arco se basa en la distancia en grados entre dos planetas o puntos importantes de una carta astral, con independencia de los signos que ocupan. Históricamente podemos distinguir tres fases en el desarrollo de este modelo.
En la primera, que se deriva en línea recta del modelo anterior, se contemplan los mismos cinco aspectos clásicos, pero dando prioridad al planeta sobre el signo. Así, dos planetas están en sextil si la distancia entre ambos equivale a la extensión de dos signos (60º), en cuadratura si están a la distancia de tres signos (90º), en trígono si están a una distancia de cuatro signos (120º) y en oposición si están a una distancia de seis signos (180º). Si no hay distancia entre ellos se dice que están en conjunción (0º). Como muy rara vez la distancia entre dos planetas coincidirá exactamente con la extensión de un número entero de signos, se admite un margen de variación a ambos lados de esa distancia, conocido actualmente con el nombre de "orbe". En el primer modelo carecía de sentido aplicar a los aspectos el concepto de orbe, pero el término existió antes de que el segundo modelo se convirtiera en dominante. Originalmente se usaba para designar una propiedad de los planetas, no de los aspectos, que definía hasta donde se estimaba que alcanzaba la influencia de sus rayos circularmente en torno del astro, y que era distinta para cada planeta. Más tarde, el término "orbe" fue aplicado directamente a los aspectos, siendo también diferente para cada uno. Actualmente algunos astrólogos combinan ambos criterios y determinan el orbe de un aspecto tanto en función del arco como de los planetas que lo conforman. La introducción del concepto de "orbe" conduce inmediatamente al surgimiento de varios conceptos relacionados. Se habla de "aspecto aplicativo" cuando el planeta más rápido se encuentra en la parte del orbe anterior al punto de aspecto exacto, es decir, cuando el orbe disminuye progresivamente y la intensidad del aspecto va en aumento. Se dice que un aspecto es partil cuando es totalmente exacto, o bien, tal como lo usan algunos, cuando es exacto dentro de un grado. Y se habla de aspecto separativo cuando el planeta más rápido se encuentra en la parte del orbe posterior al punto de aspecto exacto, es decir, cuando el orbe aumenta progresivamente y la intensidad del aspecto va disminuyendo. Por tanto, ya no estamos ante aspectos del tipo todo-o-nada, sino ante procesos graduales de formación y disolución de aspectos cuyos umbrales son difíciles de establecer.
En una segunda fase, Kepler, que no creía en los signos, pero sí en los arcos, acabó con esta dependencia del modelo anterior y decidió que los aspectos debían determinarse por criterios geométricos. El punto, la recta (el diámetro), el triángulo, el cuadrado, el pentágono, el hexágono y algunas otras figuras inscritas sobre el círculo zodiacal partiendo de la posición de un planeta, determinarían los lugares de aspecto. Irrumpen así los aspectos keplerianos derivados de la división del círculo en cinco o en diez partes iguales: el quintil (72º) y el biquintil (144º), el decil (36º) y el tridecil (108º); y los derivados de la división en ocho partes: la semicuadratura (45º) y la sesquicuadratura (135º). Morin de Villefranche añadiría el semi-sextil (30º) y el quincuncio (150º), derivados de la división del círculo en doce partes iguales, como aspectos de pleno derecho.
En la tercera fase, con John Addey entra en escena un modelo ondulatorio de los aspectos basado en resonancias armónicas que se inspira en Pitágoras, Kepler y las shodasavargas de la astrología védica. En este modelo dos planetas están es aspecto si su distancia en grados equivale al resultado de dividir el círculo por cualquier número entero o a un múltiplo de ese resultado. Cada número entero, al ser utilizado como divisor del círculo, genera tantos puntos de aspecto como indique el número del divisor. El 1 genera un único punto de aspecto, ocupado por la conjunción clásica, entendida como aspecto de 360º. El 2 genera dos puntos de aspecto: el primero queda ocupado por la oposición clásica (180º) y el segundo de nuevo por la conjunción (180º x 2). El 3 genera tres puntos de aspecto: los dos primeros se corresponden con los clásicos trígonos (120º y 120º x 2) y el tercero de nuevo con la conjunción (120º x 3). El 4 genera cuatro puntos de aspecto, a intervalos de 90 grados: el primero y el tercero se corresponden con las cuadraturas tradicionales, el segundo de nuevo con la oposición y el cuarto una vez más con la conjunción. Y así sucesivamente. Como acabamos de ver, cada división puede contener diferentes aspectos y cada aspecto puede obtenerse a partir de diferentes divisores. Así, la conjunción se obtiene a partir de la división del círculo por cualquier número entero, la oposición a partir de la división por cualquier número par, el trígono a partir de la división por cualquier múltiplo de 3, la cuadratura a partir de la división por cualquier múltiplo de 4. Y así sucesivamente.
También aquí se contempla la noción de orbe, pero aplicada exclusivamente a los aspectos. Los orbes son inversamente proporcionales al divisor del círculo que define el aspecto. Se parte de un orbe bastante generoso para la división por 1 (conjunción): 12º, 15º o más grados a cada lado del punto de aspecto exacto. A partir de ahí, el orbe de los demás aspectos se obtiene dividiendo el orbe de la conjunción por el número del divisor más bajo que genera cada aspecto. El divisor más bajo que genera la oposición es el 2; por tanto, a la oposición le corresponde la mitad del orbe de la conjunción. El trígono lo encontramos por primera vez al dividir el círculo por 3; por tanto al trígono le corresponde la tercera parte del orbe de una conjunción. Y así sucesivamente. De acuerdo con esto, la afirmación hecha más arriba de que la conjunción se obtiene a partir de la división del círculo por cualquier número entero sólo es verdadera cuando la conjunción es exacta. De otro modo, antes o después quedará fuera de orbe.
Como los números enteros son infinitos y cada uno de los sucesivos números enteros divide el círculo en porciones cada vez más pequeñas y más numerosas, resulta que, si nos tomamos esta definición al pie de la letra, cualquier distancia angular entre dos planetas acabará antes o después formando un aspecto en alguna división. Addey asume esta consecuencia y no sólo no ve motivos para preocuparse por ella sino que la considera, más bien, una virtud añadida a su modo de entender los aspectos. Lo que a Addey le parece inconcebible es la idea de que dos planetas puedan estar "incomunicados", como sería el caso si no hubiera ningún aspecto entre ellos. Pero si no queremos que la palabra "aspecto" acabe por no significar nada debemos encontrar alguna manera de distinguir unos arcos de otros por sus cualidades o por su intensidad. Addey postula que la cualidad de un aspecto depende del número usado como divisor del círculo para generarlo. Para dotar a los números de significado recurre a la numerología pitagórica y a la cábala medieval. Asigna, así, al número 9 el significado de plenitud y final de un ciclo y esto le lleva a considerar que los significados más importantes de los números están contenidos en los nueve primeros. Los aspectos resultantes de divisiones del círculo por números mayores que el nueve pueden remitirse a alguno de los nueve primeros a través de series o familias de aspectos basadas en cadenas de múltiplos. Así, por ejemplo, un aspecto de 22º 30' es generado por la división del círculo en 16 partes iguales. El 16 puede remitirse al 8, al 4 o, en último término, al 2, porque 16 es igual a 4 x 4 y a 2 x 8. Esto no cubre todo el espectro, porque los números primos mayores que nueve son irreductibles a ningún número anterior, pero nos da la oportunidad de no partir de cero en la investigación de una gran cantidad de aspectos nuevos.
La cuestión es ¿dónde nos detenemos? Porque es evidente que no podemos ampliar indefinidamente el número de los aspectos ascendiendo sin parar por la escalera infinita de los divisores enteros del círculo. Esto no sólo es inviable en la práctica sino que, además, conlleva otra dificultad. Los nuevos aspectos añadidos a partir de divisores cada vez mayores no tardarán en caer dentro del orbe de los aspectos generados por los divisores menores. El solapamiento de los orbes puede ser esquivado por algún tiempo usando orbes cada vez más pequeños, pero sólo puede evitarse por completo reduciendo a cero el orbe de la conjunción, es decir, eliminando los orbes. De lo contrario, antes o después nos encontraremos con arcos correspondientes a dos o más aspectos a la vez. Esto no ha pasado inadvertido a los partidarios de las teorías más restrictivas de aspectos y algunos de ellos lo presentan como una contradicción que necesariamente invalida la idea de que el círculo pueda ser dividido con sentido por muchos más números que los contemplados por la teoría clásica. Sin embargo, no estamos propiamente ante una contradicción inherente a una forma determinada de entender los aspectos, sino, más bien, ante una crisis de pareja entre dos modelos teóricos diferentes que han convivido por mucho tiempo bajo el mismo techo, pero que ya han llegado a un punto en el que sus caminos no convergen más y se impone una separación amistosa. Uno de estos dos modelos es el de los aspectos por signo, que enlaza los planetas indirectamente a través del contexto (signo), es categorial, cualitativo, basado en analogías visuales y corpusculares, con transiciones bruscas tipo todo-o-nada que están a la base de dicotomías excluyentes: "hay aspecto/no hay aspecto", "hay este aspecto y no otro". El otro modelo corresponde a la tercera fase de los aspectos por arco, que enlaza los planetas directamente a través de sus posiciones recíprocas (arco), está basado en analogías auditivas y ondulatorias, con transiciones graduales y patrones de vibración que no se excluyen mutuamente, sino que guardan entre si relaciones armónicas y suman o restan las ondas de los diferentes patrones con los que puede sintonizar un mismo arco.
Aunque históricamente la evolución desde el primer modelo hasta la tercera fase del segundo se ha desarrollado gradualmente a través de las dos fases intermedias, cada vez está más claro que cada enfoque habla de algo diferente. Y el solapamiento de los orbes marca el punto a partir del cual ya no pueden seguir avanzando juntos. Consideremos un ejemplo. Supongamos que tenemos una carta astral con el Sol a 3º 22' de Piscis y la Luna a 13º 34' de Cáncer. El arco Sol-Luna mide 130º 12'. De acuerdo con el primer modelo de aspectos por signo, el Sol y la Luna están en trígono, porque cada uno de ellos ocupa un signo diferente del mismo elemento. De acuerdo con las versiones más antiguas del modelo de aspectos por arco, se podría conceder un trígono con 10º 12' de orbe, dado que el orbe para los aspectos entre las luminarias se estimaba en unos 11º 30', pero pocos astrólogos modernos estarían dispuestos a aceptar un orbe tan amplio para un trígono. El veredicto de un programa de cálculos astrológicos actual, configurado con las opciones por defecto, sería que no hay ningún aspecto entre el Sol y la Luna en esta carta. Si nos aventuramos a probar con divisiones armónicas del círculo, encontramos que (360 / 11 ) x 4 = 130º 54', un aspecto de la serie del 11 que podemos denominar tetraoncil o algo parecido. La diferencia entre este aspecto y nuestro arco Sol-Luna es de 0º 42'. Si asignamos a la conjunción un orbe de 12 grados, a los puntos de aspecto derivados de la división del círculo en 11 partes iguales les corresponderá un orbe de 1º 05'. Por consiguiente, el arco Sol-Luna está dentro del orbe del tetraoncil y puede ser interpretado combinando los significados de estos dos planetas con el significado del número 11. Este es un número primo que no puede reducirse a ninguno de los 9 primeros, pero ya hay alguna investigación hecha sobre él. Se le asocia con excesos y con transgresiones, con el deseo de experimentar cosas nuevas y con el espíritu de aventura. Pero si vamos un poco más lejos, encontramos que (360 / 36) x 13 = 130º, que sólo se diferencia en 0º 12' de nuestro arco Sol-Luna. Con 12 grados de orbe para la conjunción, un aspecto derivado de la división del círculo por 36 deberá tener un orbe de 0º 20'. Tenemos, por tanto, un segundo aspecto dentro de orbe, que ahora debe interpretarse combinando los significados de las luminarias con los del número 36. Puesto que 36 es igual a 9 x 4, podemos inferir que un aspecto de esta serie indicará plenitud alcanzada a través de un esfuerzo. Pero los dos aspectos se forman entre los mismos planetas, y esto es lo que a los partidarios de los sistemas de aspectos más simples les parece tan intolerable como afirmar que un planeta se encuentra en dos lugares a la vez. La situación se ilustra gráficamente en la figura 1, que muestra cómo el Sol y la Luna se vinculan entre sí simultáneamente a través de un patrón de ondas de once crestas y otro de treinta y seis.
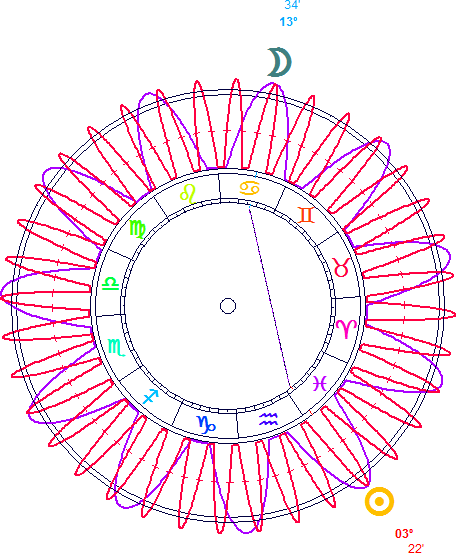
En un modelo ondulatorio dos patrones de ondas con diferentes frecuencias suman su intensidad allí donde coinciden dos crestas y la restan donde una cresta coincide con un valle. Por tanto, los dos aspectos suman aquí sus fuerzas y producen algo más intenso que si sólo estuviera uno de los dos. No tenemos que desechar uno de los dos aspectos, porque ninguno de los dos desplaza al otro. No hay que elegir entre leche o café, porque lo que tenemos aquí es café con leche. Y eso no supone ningún tipo de contradicción, aunque requiere algún entrenamiento hasta aprender a combinar las cosas en las debidas proporciones.
¿Y qué hacemos con el trígono por signo? ¿ese sí debe ser desechado o podemos tomarlo como el azúcar para el café con leche? Eso depende del valor que le demos a los signos y a los modos en que estos se clasifican. Si los consideramos exactos y valiosos, entonces el trígono por signo vendría a ser más bien la taza, el recipiente en el que se realiza la mezcla. En este caso, crearía las condiciones favorables para que los otros dos aspectos y los planetas que los conforman integren sus energías y significados de la manera más armoniosa posible. Pero podemos pensar en un escenario completamente diferente. Por ejemplo, un planeta a 0º 30' de Aries y otro a 29º 30' de Cáncer están separados por un arco de 119 grados que corresponde a un trígono dentro de un grado de orbe; pero el aspecto por signo es una cuadratura. Entonces podría darse una situación parecida a la tragedia de Romeo y Julieta. Los planetas mantienen entre sí una buena relación por arco, están enamorados (trígono, análogo a casa V), pero pertenecen a familias que están enemistadas (signos en cuadratura). Por eso la tendencia natural del aspecto por arco no encuentra condiciones favorables para su realización. Combinando los dos modelos obtenemos una imagen más exacta de la situación que excluyendo uno de los dos. Y con esto no estoy proponiendo nada nuevo, porque esta combinación de relaciones entre planetas basadas en los signos que ocupan y relaciones basadas en el arco que los separa ha cristalizado ya en la astrología en la conocida distinción entre aspectos plenivalentes y aspectos no plenivalentes. Si el aspecto por signo y el aspecto por arco son el mismo se dice que el aspecto es plenivalente; en caso contrario es no plenivalente. Pero esta distinción sólo vale para los aspectos clásicos y es propia de las primeras fases intermedias de la evolución de la teoría de los aspectos, en las que todavía podían convivir más o menos apaciblemente una al lado de la otra las dos formas de entenderlos. De hecho, es fruto del intento de hacer posible esa convivencia. Pero tan pronto como rompemos el marco zodiacal que estructura la eclíptica en sectores de 30 grados y acoge de manera natural los aspectos clásicos, porque surgieron de ese mismo marco, los dos modelos ya no pueden seguir caminando juntos por más tiempo. No hay sitio en el viejo edificio para las nuevas generaciones de aspectos, que deben independizarse y buscarse un nuevo hogar.
Todavía en la forma en que John Addey trata su propia teoría de los aspectos y en su diseño de una carta armónica se aprecia el lastre de los modelos anteriores, de los que nunca pudo, supo ni quiso desembarazarse del todo. Está pendiente la coronación del impulso que condujo hasta los armónicos en una nueva fase que prescinda del zodiaco y de los aspectos clásicos y sustituya todo eso por divisiones de la eclíptica a la medida de las nuevas series de aspectos y a los aspectos mismos por patrones ondulatorios o familias de secuencias rítmicas. Algo se ha avanzado ya en esa dirección, porque los diales de Ebertin, Wangemann, Landscheitdt y otros son básicamente cartas de los armónicos 4, 12 y 48 sin signos ni casas, pero ninguno de ellos ha generalizado el procedimiento ni lo ha presentado en el marco de una visión sistemática de la totalidad de los armónicos.
Aparentemente, los aspectos surgieron de los signos del zodiaco y de las categorías usadas para formar grupos de signos con características comunes, pero poco a poco se fueron independizando de sus ancestros y engendraron sus propios hijos. Sin embargo, si consideramos el asunto con más detenimiento nos daremos cuenta de que las divisiones armónicas de última generación son más antiguas que los propios signos y sus categorías o, al menos, lógicamente anteriores. En efecto, en el cielo hay planetas y estrellas, pero no hay divisiones naturales de 30 grados. Para introducir estos signos de igual tamaño hay que dividir el círculo de la eclíptica por un número entero, en este caso el 12. Esta operación coincide con el primer paso que se da para construir una carta del armónico 12, pero después toma otro camino: asigna una cualidad diferente a cada una de las partes y da un nombre propio a cada una de ellas. No es todavía una división armónica propiamente dicha, porque lo que caracteriza a una división armónica es que reproduce en las partes la estructura del todo. ¿Por qué se usó el número 12 para dividir la eclíptica en partes iguales? La hipótesis más verosímil es que esto se hizo porque en el tiempo que el Sol emplea en dar una vuelta completa a la eclíptica (un año) se encuentra con la Luna doce veces. Pero el ciclo sinódico lunar cabe 12,37 veces en un año, de modo que algunos años tendrán trece lunas nuevas. Parece que la división por 12 no es más que una simplificación, un redondeo al entero más cercano para organizar el calendario en doce meses por año. Pero si sólo es eso, entonces los límites exactos de los signos y hasta su existencia misma se vuelven muy cuestionables, a menos que los antiguos astrólogos tuvieran algún conocimiento de las propiedades armónicas de los ciclos. Las evidencias de que lo tenían son muchas.
En el Astronomicon de Marcus Manilius, compuesto hace más de dos mil años, podemos leer:
"observa ahora un hecho (...) que solamente puedo designar con el nombre original griego: la Dodecatemoria. (...) los Signos están formados por 30 grados cada uno. Estos los dividimos en 12 partes: el resultado será de 2 ½ grados cada parte. La Dodecatemoria viene indicada por este valor, y hay por tanto 12 Dodecatemorias en cada Signo. El Creador del mundo ha atribuido otras tantas a los brillantes Signos, para que la combinación pueda ser alterna, y que el universo se asemeje a sí mismo, y que todos los signos se incluyan en cada uno de ellos, de modo que el cuerpo esté en armonía mediante esta combinación y que el control mutuo exista como razón común de todos."
Aquí están ya presentes todos los principios de la construcción de las cartas armónicas: la división del círculo en partes iguales y la reproducción de la estructura del todo en cada parte. La única diferencia con una carta del armónico 12 al estilo de Addey es que en las Dodecatemorias el primer sub-signo de cada signo no es siempre Aries, sino que coincide con el Signo mayor en el que se aloja, y, a partir de ahí, sigue la secuencia zodiacal normal. Las Dodecatemorias son aún más sofisticadas que una carta armónica simple, porque en ellas va implícita la idea de que cualquier signo podría ser tomado como el primero del zodiaco. Si hacemos comenzar el zodiaco, por ejemplo, en Capricornio, el primer sub-signo del armónico 12 será Capricornio, el segundo Acuario, y así sucesivamente. Y lo mismo con los demás signos. Por tanto, una Dodecatemoria es un complejo artefacto que combina en una misma carta fragmentos de doce cartas armónicas distintas calculadas desde diferentes puntos de origen.
En la misma obra, Manilius nos presenta una versión de los Decanatos que coincide completamente con la forma en que se estructura el zodiaco en una carta moderna del tercer armónico. Primero se divide el círculo en tres partes iguales de 120 grados cada una y luego se aloja en cada parte un zodiaco completo, partiendo siempre desde Aries y siguiendo la secuencia natural, a razón de un signo cada diez grados. Subyace aquí la idea de que cada tercio del año reproduce a escala menor el año entero y esa misma idea está también implícita en la clasificación de los signos por elementos. La organización del Zodiaco en los Cuatro Elementos también comienza dividiendo la eclíptica en tres partes iguales, pero en lugar de alojar un zodiaco en cada parte se instala en ella una secuencia elemental: Fuego, Tierra, Aire y Agua. Cada tercio del año reproduce las cuatro partes del año. En las Modalidades, también conocidas como Cualidades o Impulsos, primero se divide el círculo en cuatro partes iguales y después se aloja en cada parte una triple secuencia cualitativa. Y en las Polaridades o Sexos se divide primero en seis y después en dos.
Por tanto, son los principios de división armónica los que organizaron el zodiaco en los Elementos, Impulsos y Polaridades, de los que se derivaron luego los aspectos. Lo único que hace la Teoría de Armónicos moderna es ahorrarles a los aspectos ese rodeo y derivarlos directamente de las divisiones armónicas. De ese modo se abre ante nosotros un vasto territorio de exploración y, con él, numerosas incógnitas e incertidumbres. ¿Hasta dónde podemos ascender por la escalera de los números enteros usados como divisores del círculo?, ¿Cómo interpretar las nuevas series de aspectos?, ¿Qué peso o importancia podemos atribuir a los aspectos derivados de divisores altos?, y muchas otras.
Un aspecto clásico visto a través de las lentes de aumento de una cadena relativamente amplia de divisores armónicos aparece como un tejido con la forma de una confederación de micro-aspectos y presenta una curiosa propiedad que podemos denominar "el centrifugado de los puntos de aspecto". Esto consiste en lo siguiente. Imagine que dispone de una "carta astral virgen", es decir, de una copia impresa de un círculo graduado que contiene solamente un zodiaco, y se propone marcar sobre ella los puntos de aspecto correspondientes a unos cuantos divisores enteros, empezando por el 1 y avanzando por orden de unidad en unidad. El primer punto de aspecto y el único que contiene la primera serie lo marcaremos a cero de Aries, dibujando, por ejemplo, un pequeño círculo a la altura de ese grado por la parte exterior de la carta. La división por 2 genera dos puntos de aspecto, el cero de Aries, que es común a todas las series, y el cero de Libra. Dibujamos una segunda marca en cero de Aries y una nueva en cero de Libra. La división por 3 dejará marcas a cero grados de cada signo de Fuego, la división por 4 a cero grados de cada signo cardinal, la división por cinco a intervalos de 72 grados, y así sucesivamente. Cuando haya completado las 12 primeras series, tendrá 12 marcas en 0º de Aries (conjunción), 6 en 0º de Libra (oposición), 4 en 0º de Leo y otras 4 en 0º de Sagitario (trígonos), 3 en 0º de Cáncer y otras 3 en 0º de Capricornio (cuadraturas), 2 en 12º de Géminis, 24º de Leo, 6º de Escorpio y 18º de Capricornio (quintiles y biquintiles) y otras 2 en 0º de Géminis y 0º de Acuario (sextiles). Además habrá otras 34 marcas individuales diseminadas a lo largo del círculo, pero ninguna de ellas quedará demasiado cerca de los puntos donde se han acumulado mayor número de marcas (figura 2).
Como norma general, cuantas más marcas se acumulen en un determinado punto menos marcas se acumularán en las zonas inmediatamente adyacentes. La figura 2 representa el modo en que se distribuyen las 78 marcas de las 12 primeras series sobre un total de 46 puntos de aspecto. Los grados que son puntos de aspecto en mayor número de divisiones son los que coinciden con los que la teoría clásica considera aspectos mayores, con el añadido de los quintiles y biquintiles. A ambos lados de estos aspectos mayores aparecen zonas vacías, como si hubieran sido despejadas por un efecto de centrifugado de puntos de aspecto que se van acumulando cerca de los bordes exteriores de esas zonas. A medida que seguimos añadiendo nuevas series de puntos de aspecto, las zonas vacías van reduciendo su tamaño y acabarían por desaparecer si continuáramos añadiendo series indefinidamente. Pero así como el oído humano no puede captar frecuencias por encima o por debajo de ciertos valores de hertzios, es de esperar que las series de aspectos se vuelvan ineficaces más allá de ciertos límites. Mi propia investigación experimental en el campo de la sinastría ha arrojado ciertos resultados que sugieren que esos límites existen y dan pistas muy concretas de dónde pueden estar.
En el artículo titulado Orbes heliocéntricos y formación de parejas, donde analizo algunos detalles de la comparación de las cartas natales de cerca de tres millares de matrimonios, he registrado datos sobre conjunciones partiendo de un orbe muy amplio, de 13º 20'. Después probé a dividir este orbe en dos partes iguales y observar por separado las conjunciones entre 0º y 6º 40' y las conjunciones entre 6º 40' y 13º 20'. Al hacerlo de esta manera se hizo evidente que había más actividad (más contactos entre planetas de los dos miembros de cada pareja) en la zona de conjunciones de orbe más estrecho. Esto es lo que cualquier astrólogo hubiera esperado que sucediera, porque se asume que cualquier aspecto será tanto más fuerte cuanto más cerrado sea el orbe. Entonces di un paso más, y decidí dividir también en dos partes iguales las conjunciones de orbe estrecho, observando por separado las conjunciones entre 0º y 3º 20' y las conjunciones entre 3º 20' y 6º 40'. Y aquí me llevé una sorpresa, porque la actividad registrada era claramente superior entre 3º 20' y 6º 40', prácticamente con todos los planetas y con independencia de si usaba posiciones geocéntricas o heliocéntricas. En los 3º 20' inmediatamente antes o después del punto de conjunción exacta no se observaba nada por encima de lo normal, parecía un área inactiva, y el efecto era demasiado persistente en esa muestra como para atribuirlo a la casualidad. Esto es lo contrario de lo que la forma convencional de pensar en los aspectos permitía esperar. Ante resultados como éste, la teoría clásica de los aspectos se queda demasiado corta y enmudece de perplejidad, pero la teoría armónica de los aspectos puede al menos proponer alguna explicación.

Pulse sobre el gráfico si desea verlo ampliado
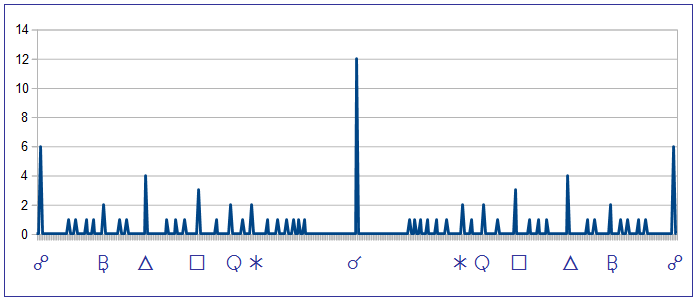
La parte superior de la figura 3 muestra la distribución de los puntos de aspecto correspondientes a las 108 primeras divisiones armónicas desde unos 10 grados antes del punto de conjunción hasta unos 10 diez grados después. La parte inferior de la figura sólo es una ampliación de la mitad derecha del mismo espectro mostrado arriba. Se aprecia claramente el efecto de centrifugado de los puntos de aspecto al que me he referido antes. En el lugar exacto de la conjunción se acumulan 108 puntos que conforman la línea central, pero en los 3º 20' inmediatamente anteriores o posteriores no hay absolutamente ningún otro punto de aspecto. Sin embargo, pasado ese límite los puntos de aspecto no se distribuyen de manera homogénea, sino que se aglomeran muy cerca del límite, como si hubieran sido empujados desde las zonas vacías unos contra otros. De este modo se acumulan más puntos de aspecto entre los 3º 20' y los 6º 40' que de ahí en adelante y, por supuesto, muchos más que entre 0º y 3º 20', donde solamente hay uno, aunque sea muy intenso. Esto puede explicar muy bien por qué en mi investigación sobre aspectos en parejas se detectó mucha actividad entre 3º 20' y 6º 40', menos entre 6º 40' y 13º 20' y prácticamente ninguna entre 0º y 3º 20', pero sólo si suponemos que, al menos en lo que concierne a las relaciones de pareja, el límite máximo de divisiones del círculo eficaces está en torno a unos 108 armónicos.
Este efecto de centrifugado de los puntos de aspecto también se observa en los alrededores de la oposición, del trígono y de la cuadratura, pero con áreas vacías proporcionalmente menores y puede ayudar a entender por qué prácticamente en ninguna investigación estadística sobre aspectos se observan máximos coincidentes con aspectos partiles. Por ejemplo, Robert Hand, en su libro Los símbolos del horóscopo, p. 123, comenta a propósito de los orbes:
Ciertas investigaciones indican que el efecto vinculante culmina un poco antes del punto de exactitud, mientras que en el trabajo presentado por Gary Duncan, de California, en la convención AFA de 1976 se indica que en el caso de las cuadraturas, por lo menos, la vinculación máxima se da a veces después del punto exacto. Y el trabajo con armónicos sugiere que es probable que la intensidad no decline de forma lineal, sino que el efecto vinculante se eleve y descienda en diversos puntos a medida que el aspecto se va moviendo hasta salir del orbe.
En efecto, tanto el análisis teórico de la combinación de patrones de ondas como los resultados experimentales disponibles sugieren que la distribución de la intensidad dentro de la franja considerada habitualmente como el orbe apropiado para un aspecto mayor es probable que se pareca más a la curva azul de la figura 4 que a la curva roja. Esta última representa el modo en que se suele pensar en el orbe de un aspecto, porque parece lógico que la intensidad aumente progresivamente hasta el punto de exactitud y luego decline de la misma forma. Y en efecto, así es como cabe esperar que sucedan las cosas dentro de un patrón de ondas aislado de todos los demás, pero como los diferentes patrones o trenes de ondas se afectan mutuamente y en las zonas correspondientes a los aspectos mayores se da el fenómeno de centrifugado de puntos de aspecto, en la práctica encontraremos distribuciones más parecidas a la línea azul.
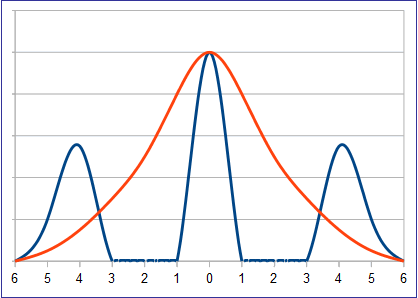
De hecho, la misma tradición astrológica nos ha legado un esquema muy parecido a éste, en lo que se refiere a las conjunciones del Sol, porque, como nos recuerda Demetrio Santos, se dice que "un planeta está combusto cuando está a menos de 3 grados de distancia angular del Sol" (Textos astrológicos medievales, Madrid, 1981, p.243), y Nicholas Devore, aunque se hace eco de otras opiniones que extienden la combustión hasta los 8º30', añade: "El efecto característico al que se aplica el término probablemente se reduce dentro de un arco de 3º" (Enciclopedia astrológica, Buenos Aires, 1972, p. 107). Ese efecto característico consiste en que el planeta que se encuentra a menos de tres grados del Sol queda "perjudicado", como quemado por sus rayos, y aunque no deja de actuar, lo hace de una manera poco receptiva, rígida e independiente de la visión integradora solar. De este modo funciona como si no estuviera en aspecto con el Sol, pero si se acerca a menos de 0º 17' del Sol, se dice entonces que el planeta está Cazimi, es decir, en el corazón del Sol, y entonces, curiosamente, deja de quemarlo y perjudicarlo y lo eleva a una gran dignidad real que le hace funcionar del modo más excelso. Por unos cuantos grados más allá de la zona de combustión se dice que el planeta está "bajo los rayos", y ahí funciona como estando en conjunción normal con el Sol. Si compara la figura 5 con la línea azul de la figura 4 apreciará la gran similitud del esquema tradicional de las conjunciones solares con el modelo de orbes de suma de ondas a la altura de 108 armónicos.
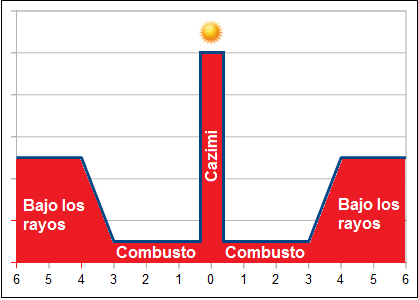
Una vez que un planeta entra dentro del orbe de conjunción con el Sol se aprecia un vínculo entre ambos que se mantiene hasta que la distancia baja de unos 3 grados; entonces el planeta "se desconecta" del Sol por un tiempo y vuelve a conectarse súbitamente con él y del modo más impresionante cuando la distancia se reduce por debajo de los 17 minutos de arco. Es exactamente lo que predice la teoría de la suma de ondas si le ponemos un límite cercano al centenar de series, porque entonces habrá un primer pico poco antes de los tres grados, intenso pero algo disperso, ya que muchos puntos de aspecto se acumulan en la misma zona, pero no en el mismo lugar. Después entraremos en una zona de sombra, en la que no se aprecian resonancias ni vínculos, hasta que la conjunción sea partil. En ese momento se disparará súbitamente la intensidad del vínculo, tras la calma que precede a la tormenta, y luego decaerá abruptamente por unos tres grados. Finalmente se formará otro pico de intensidad similar a la del primero.
Parece que el esquema tradicional de las conjunciones solares -atribuido a la acción de sus rayos sobre otro planeta con dudosa lógica, porque si a tres grados se quema a cero tendría que abrasarse- ha sido una anticipación del complejo modelo de variación de intensidad en el interior del espacio del orbe de los aspectos mayores que se deriva de la lógica de los armónicos. Pero el modelo de los aspectos desde el punto de vista de la Teoría de los Armónicos no se apoya en la luz, sino en el sonido. Su referencia mística es la pitagórica música de las esferas. Por tanto, no es una cuestión de rayos, sino de vibración y lo que importa no es la luz, sino la distancia. Si la luz fuera tan decisiva, los planetas situados por debajo del horizonte no nos afectarían. Pero así como podemos escuchar a una persona que nos habla del otro lado de una puerta, aunque no podamos verla, podemos sintonizar con los planetas que están debajo del horizonte aunque no nos llegue su luz. No puede entonces extrañarnos que el mismo esquema general de variaciones de intensidad que los antiguos astrólogos detectaron en torno al Sol y sus conjunciones pueda trasladarse también a otros planetas y otros aspectos. Tenemos ya alguna evidencia empírica de que esto es así, por lo menos en el caso de las conjunciones y en el campo de la sinastría, pero falta aún mucha investigación adicional para poder asegurar que algo semejante sucede también con otros aspectos y en otros campos. En teoría, una investigación minuciosa debería detectar estas áreas silenciosas inmediatamente antes y después del punto de aspecto exacto también en las oposiciones, los trígonos y las cuadraturas, pero en cada uno de estos aspectos las zonas de inactividad deben ser proporcionalmente menores, la mitad de grados para la oposición, un tercio para el trígono y la cuarta parte para la cuadratura. Así, cada vez quedan más cerca del punto de aspecto exacto y se prolongan por menos tiempo, de modo que hay que hilar muy fino para organizar un método de análisis capaz de detectarlas.
Lo fundamental es que nos demos cuenta de que dentro del orbe de los aspectos mayores habitan muchos aspectos diferentes en cualidad, en número y en intensidad, que sólo se hacen visibles mirados a través del microscopio de los armónicos, en sucesivas ampliaciones. Todas las ciencias naturales han progresado así, penetrando cada vez más profundamente en la estructura íntima de la materia, sus células, moléculas, átomos y partículas subatómicas. Los armónicos nos brindan la oportunidad de estudiar la composición interna de los aspectos clásicos y de descubrir aspectos nuevos dentro y fuera de ellos. Para avanzar por este camino se necesitan instrumentos adecuados, como las cartas armónicas, incorporadas ya prácticamente a todos los programas de cálculos astrológicos de mediana complejidad, o los armogramas, disponibles en el programa Armon de Miguel García. Se echaba en falta, no obstante, una utilidad rastreadora de aspectos de amplio espectro, pero gracias a Sylvia de Ayala (webmaster de Carta Natal online), que ha tenido la amabilidad de atender una sugerencia mía al respecto, disponemos ahora de un explorador de aspectos, prácticamente sin límite de series.
El funcionamiento de esta utilidad es bastante sencillo, siempre que se tengan claros los conceptos básicos. Es necesario, pues, comenzar aclarando qué entendemos aquí por "serie de aspectos", porque la expresión ha sido empleada con un sentido diferente por otros autores. David Hamblin hace notar que todos los armónicos que forman una cadena de potencias a partir de un número primo constituyen una serie. La serie del Dos está formada por los números 2, 4 (2 x 2), 8, (2 x 2 x 2), 16 (2 x 2 x 2 x 2), etcétera, la serie del Tres incluye los números 3, 9 (3 x 3), 27 (3 x 3 x 3), 81 (3 x 3 x 3 x 3), etcétera. Y así sucesivamente con los demás números primos. No habla de series de aspectos, sino de series de armónicos, pero, como cada armónico lleva asociado un grupo de aspectos, Robert Hand da el paso siguiente y decide clasificar los aspectos más utilizados en dos categorías. Escribe Hand:
"Excepción hecha de la conjunción, a todos los aspectos comúnmente usados se los puede clasificar de acuerdo con que estén basados en múltiplos de dos o de tres. (...) La familia de aspectos basados en la división del círculo por dos incluye la oposición (1/2), la cuadratura (1/[2 x 2] o 1/4), la semicuadratura (1/[2 x 2 x 2] o 1/8) y la sesquicuadratura (3/8), así como todos los múltiplos de 22,5º (1/[2 x 2 x 2 x 2] o 1/16). Yo los llamo "aspectos de la serie del dos" o "aspectos duros". (...) La familia de los aspectos basados en la división del círculo por tres incluye el trígono (1/3), el sextil (1/[3 x 2] o 1/6), el semisextil (1/[3 x 2 x 2] o 1/12) y el quincuncio (5/12). Yo los llamo "aspectos de la serie del tres" o "aspectos blandos". La conjunción constituye una clase por sí misma, porque podría estar en la serie del dos, en la serie del tres o en cualquier otra serie de aspectos.".
Su definición de los aspectos de la serie del dos sigue la pauta marcada por Hamblin y se atiene a las divisiones del círculo por potencias de dos. Sin embargo, los aspectos que Hand incluye en su serie del tres no son los derivados de las divisiones del círculo por potencias de tres, sino los derivados de la división por tres o por múltiplos de tres que no sólo no son potencias de tres sino que son también múltiplos de dos. El sextil se deriva del 6, que es múltiplo de 2 y de 3 a la vez, y los semisextiles y quincuncios se derivan del 12, que tiene más participación en el 2 que en el 3. Por tanto, lo que Hand llama "serie del tres" es una serie mixta del dos y del tres.
Menciono todo esto para que aquellas personas que hayan leído a Robert Hand sepan que deben dejar a un lado su manera de definir las series de aspectos cuando se dispongan a utilizar el explorador de aspectos de Carta Natal online. Lo que entendemos por serie de aspectos de N dentro del explorador es el conjunto de todos los múltiplos de 360 / N. Así, por ejemplo, la serie del 5 comprende todos los múltiplos de 360 / 5 que caben dentro del círculo, es decir, 72º, 144º, 216º, 288º y 360º. Los arcos de 72º y 288º (quintiles) indican, en realidad, el mismo ángulo de separación entre dos planetas, medido en el primer caso por la distancia más corta y en el segundo por la más larga. Y otro tanto ocurre con los arcos de 144º y 216º (biquintiles). El arco de 360º es la conjunción medida por su distancia más larga. Se puede decir, pues, que la serie del 5 incluye los quintiles y los biquintiles, además de la conjunción, que pertenece a todas las series. Pero el número total de puntos de aspecto es 5, porque partiendo del lugar ocupado por un planeta A habrá cinco lugares en el zodiaco desde los que un planeta B podrá hacer un aspecto exacto de la serie del 5 con el planeta A. El número de puntos de aspecto es siempre igual al número de la serie, de modo que cuanto más alta sea la serie más puntos de aspecto habrá. Sin embargo, esta profusión de puntos de aspecto en las series altas no incrementa la probabilidad de que entre dos planetas cualesquiera se forme un aspecto, porque los orbes se reducen de manera proporcional al número de la serie. De este modo, la relación entre el área total del zodiaco dentro del orbe de los aspectos y el área fuera de esos orbes permanece constante en todas las series. Esto es fundamental para poder comparar unas series con otras y localizar, así, indirectamente los armónicos más fuertes (con más conjunciones internas) de una carta natal. Por eso, nos detendremos un poco más en el tema de los orbes.
El explorador de aspectos solicita al usuario un número de serie y un orbe. El número de serie, como ya sabe, es el número de partes iguales en que vamos a dividir el círculo para definir una serie de aspectos: 5 para buscar quintiles y biquintiles, 7 para hallar septiles, biseptiles y triseptiles, etcétera. El orbe que se solicita, sin embargo, no es el orbe específico para la serie elegida, sino el orbe general para todas las series. A partir de ese orbe general, el explorador hará los ajustes oportunos en cada serie. Se podría decir que el orbe general coincide con el de la conjunción en la serie del 1, cosa que es exacta, pero creo que es mejor pensar en el orbe general como la suma de los orbes de todos los puntos de aspecto de cada serie. En realidad es lo mismo, pero esta segunda manera de enfocarlo puede ayudar a superar la resistencia que muchos astrólogos experimentan a conceder a la conjunción el doble de orbe que a la oposición y cuatro veces el de una cuadratura. Es posible que, en realidad, la conjunción no tenga tanto orbe, pero eso no importa mucho aquí. La cuestión es que para poder comparar las series eficazmente debemos actuar como si lo tuviera. Además, el explorador de aspectos no se ha diseñado para localizar conjunciones, porque es muy fácil detectarlas a simple vista. Se ha diseñado para localizar aspectos pequeños y compararlos con otros en igualdad de condiciones. Por tanto, sea generoso al asignar el orbe general. Por ejemplo, 16 grados no es en absoluto un orbe general excesivo. Piense que esos 16 grados habrá que repartirlos entre todos los puntos de aspecto de cada serie. La cuadratura, por ejemplo, pertenece a la serie del 4, que incluye todos los múltiplos de 90º. Pero como la serie del 4 tiene 4 puntos de aspecto, si el orbe general es 16º a cada punto le corresponderán 4º. Si usted piensa que 4º es un orbe apropiado para una cuadratura entonces mantenga el orbe general en 16º. Si le parece poco, amplíe aún más el orbe general; si le parece mucho, redúzcalo.
Una cuadratura de 4 grados de orbe en la carta natural o armónico 1 se ve en el armónico 4 como una conjunción de 16 grados de orbe, por lo que no puede aceptar una cosa y rechazar la otra. Lo que se ve en ambos armónicos es lo mismo, sólo que mirado a través de diferentes lentes de aumento. Probablemente la razón por la cual la idea de que la conjunción tiene el doble de orbe que la oposición genera tanta resistencia es que en la práctica las conjunciones que superan el orbe de la oposición son muy difíciles de detectar. En efecto, la conjunción dentro de su propia serie y en su propio armónico (el 1) tiene una frecuencia demasiado baja, que hace que sólo sea reconocible a partir del momento en que empieza a sumar fuerzas de otras series y armónicos más altos. Pero tan pronto como esto ocurre, ya desde la serie del 2, el orbe de la conjunción se reduce a la mitad, por lo que la parte del orbe de la conjunción que rebasa el orbe de una oposición nunca recibe ningún aporte suplementario de energía. Sin embargo, esto no se aplica a las conjunciones dentro de una carta armónica distinta de la primera, porque lo que estamos viendo en esas cartas como conjunciones son, en realidad, los aspectos de la serie correspondiente. Y cuando esos aspectos están cerca del límite de su orbe se verán como conjunciones con un orbe más amplio que el que está acostumbrado a aceptar en una carta natural. Pero ese es el orbe adecuado, son sus hábitos de percepción de aspectos los que tienen que reajustarse cuando mira una carta armónica, no los orbes.
Cada serie de aspectos lleva asociado un patrón de ondas y un armónico. Cuando aparecen muchos aspectos en una serie podemos asumir que el nativo de esa carta sintoniza fuertemente con un patrón de ondas con tantas crestas como indique el número de la serie y que la carta armónica del mismo número tendrá tantas conjunciones dentro del orbe general como aspectos haya en la serie. Tal vez se esté preguntando cuántos aspectos debe haber en una serie para poder decir que son muchos. Eso depende del orbe general elegido y del número de planetas o factores que se tengan en cuenta. En el caso de Albert Einstein, por ejemplo, con un orbe general de 16º y con los diez planetas que, por ahora, incluye el explorador, la media de aspectos de las 50 primeras series es 3,82. Todas las series tienen al menos un aspecto y dos de ellas, la 10 y la 49, tienen siete. Pero en esas mismas condiciones, la serie del 48 de Aron Ralston alcanza 15 aspectos. El número de aspectos de una serie es un criterio muy tosco para valorar la fuerza de la carta armónica aparejada; sin embargo, nos da una pista importante y es aconsejable mirar las cartas armónicas del mismo número que las series con más aspectos. Como se ha dicho ya, cada aspecto de una serie aparecerá como conjunción en su armónico correspondiente, pero el armónico será mucho más fuerte si esas conjunciones están agrupadas que si están salpicadas por toda la carta. Cuando varios planetas se agrupan en pocos grados dentro de una carta armónica formarán una configuración cerrada de aspectos de la serie correspondiente en la carta natal natural. En el artículo Aspectos menores de efectos mayores. Una aproximación al armónico 48 y sus aspectos asociados he presentado varios ejemplos de cómo sacar partido de la combinación de las series de aspectos con las cartas armónicas. Además, como señaló David Hamblin, las cartas armónicas se relacionan unas con otras a través de cadenas de potencias y de múltiplos, por lo que también las series de aspectos se pueden agrupar en familias. Los linajes más puros siguen la línea de las potencias. Así, por ejemplo, la serie del 49, que es una de las más destacadas en la carta de Albert Einstein, está directamente emparentada con la serie del 7, ya que 49 es 7 al cuadrado. Si los aspectos de la serie del 7 se relacionan con la inspiración, las ideas luminosas y la genialidad, los de la serie del 49 (7 x 7) elevarán estas características a una potencia superior.
Por último debo aclarar que el uso que se hace en este artículo de los modelos ondulatorios y su relación con los armónicos en astrología y las series de aspectos asociadas a ellos es meramente metafórico. Sólo se trata de un recurso didáctico que creo que puede ayudar a entender cómo funcionan los armónicos en astrología, pero no se asume la existencia real de tales ondas físicas ni que las analogías puedan llevarse más allá de ciertas generalidades.
© 2014, Julián García Vara
Encontrará textos originales de John Addey y mucha más información adicional en la siguiente dirección:
Armónicos en astrología. Recopilación de textos
Autor: Julián García Vara
Blog: https://astrologia-viva.blogspot.com.es
Este artículo pertenece a su autor y puede tener algunos derechos reservados.
Consulte con el autor para su publicación

